Random Walk and the Arcsine Law: Why Extremes Are More Common Than You Think
Have you heard of a random walk (in English they even say “drunkard’s walk”) and the arcsine law? These concepts mess with your head because they describe something that contradicts literally everything your gut tells you about how randomness works.
What Is Random Walk?
In math terms, it’s just a sequence of steps where each move has a 50% chance of going up or down. Each one fair, independent, unbiased. But if you plot the results, the path doesn’t hover neatly around zero. It wanders off. Once it picks a direction, it usually sticks to it for a while.
The longer the random walk continues, the further it tends to drift from where it started. After 100 steps, there’s a high chance you’re far from zero. The further away you get, the less likely you are to come back quickly. Statistically, the walk will spend most of its life wandering off in one direction, often for long stretches before ever crossing back.
This creates these long stretches where you’re consistently on one side of the starting point. Just because that’s what happens when you let randomness run its course. The walk goes wandering off in one direction and stays there for a while.
The Arcsine Law: The Shape of Randomness
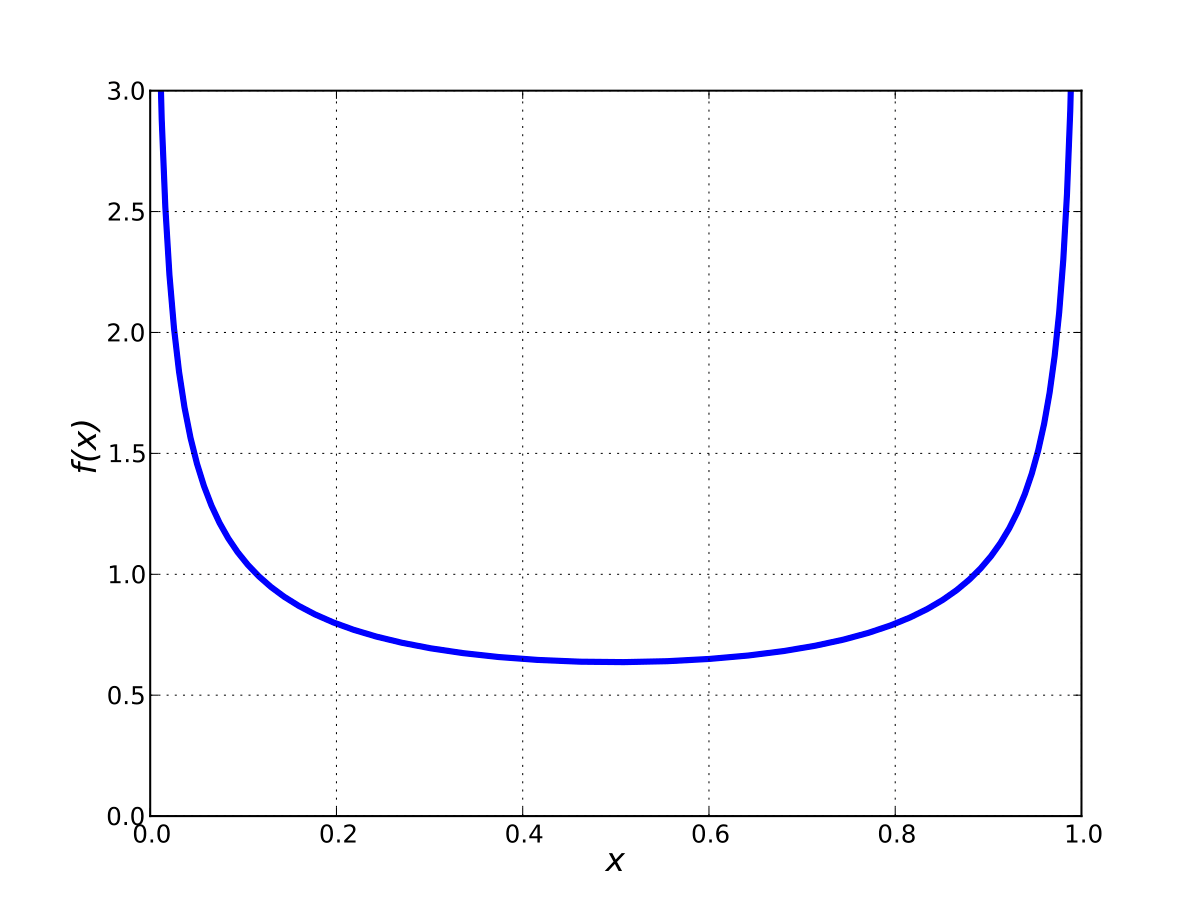
Here’s where it gets weird. The arcsine law describes how often you’re on one side versus the other during a random walk. And the answer is: way more often than seems reasonable.
Most of the time you’ll see something like 80-20 or 90-10, not 50-50. The math here follows a specific curve called the arcsine distribution, it looks like a U. The extremes are way more likely than the middle.
Here’s an example. Flip a fair coin 100 times. You might imagine 50 heads, 50 tails is the most likely result. Actually, outcomes like 80 heads and 20 tails together are more likely than a perfect balance.
That’s how runs emerge. In sports, it’s why one team can lead for most of the match even if both are evenly matched. Randomness itself guarantees long stretches of one side prevailing. The moments that matter - the lead changes, the reversals - often happen early or late. The middle is mostly monotone.
The Practical Part
You can see the same shape in business or career progress. Suppose your team has people of roughly equal skill. Performance jumps around from project to project. Some weeks everyone struggles, some weeks someone crushes it. But the person who happens to start with a few small wins often rides that momentum for months. Their wins attract opportunities, attention, and confidence. Others start slow, get stuck, and feel permanently behind. Equal skill. Unequal sequence. The arcsine law at work.
In markets, you feel it too. You invest on a random cycle. If your first few months are negative, that stretch might drag longer than seems fair. Not because something’s wrong, but because random walks don’t reset after each drop. They cluster. You can go months or years with one side dominating.
Even simple coin flip experiments show the same truth. Simulate ten thousand 100-step walks. Count how often a walk spends more than 80 percent of its life above zero. You’ll find it happens roughly one-third of the time. One out of three random sequences shows that level of dominance without bias in the system.
This law appears everywhere - from renewal theory to physics to stock prices to employee performance curves. Even daily mood swings follow it. Your brain’s emotional “walk” can stay above or below neutral longer than your intuition expects. A few good days make more good days likely for no logical reason other than the arcsine geometry of variance itself.
What fascinates me most is how this clashes with how we think fairness should look. Human intuition imagines symmetry. We expect randomness to alternate like a rhythm. In truth, randomness is streaky. It clumps. It makes luck look personal and outcomes feel earned or cursed.
See It Yourself
I made an interactive thing where you can watch this happen in real time. Play with different numbers of steps. Change the starting conditions. Watch the walk wander off in one direction and stay there. The source code is here if you want to mess with it yourself.
Here’s the thing: randomness creates extremes. It creates long winning and losing streaks. It creates situations where one outcome dominates for months or years. And it is not about an unfair game, it’s because balance and fairness aren’t what random processes naturally produce. They produce long runs. They produce wild swings. They produce the messy, streaky reality we actually live in.